Limit Calculator With Steps
Limit calculator helps you find the limit of a function with respect to a variable. This limits calculator is an online tool that assists you in calculating the value of a function when an input approaches some specific value.
Limit calculator with steps shows the step-by-step solution of limits along with a plot and series expansion. It employs all limit rules such as sum, product, quotient, and L'hopital's rule to calculate the exact value.
You can evaluate limits with respect to \(\text{x, y, z, v, u, t}\) and \(w\) using this limits calculator.
That’s not it. By using this tool, you can also find,
- Right-hand limit (+)
- Left-hand limit (-)
- Two-sided limit
How does the limit calculator work?
To evaluate the limit using this limit solver, follow the below steps.
- Enter the function in the given input box.
- Select the concerning variable.
- Enter the limit value.
- Choose the side of the limit. i.e., left, right, or two-sided.
- Hit the Calculate button for the result.
- You will find the answer below the tool.
- Use the Reset button to enter new values and the Keypad icon
to enter additional values.
What is a limit in Calculus?
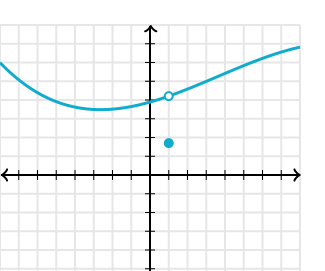
The limit of a function is the value that f(x) gets closer to as x approaches some number. Limits can be used to define the derivatives, integrals, and continuity by finding the limit of a given function. It is written as:
\(\lim _{x\to a}\:f\left(x\right)=L\)
If f is a real-valued function and a is a real number, then the above expression is read as,
the limit of f of x as x approaches a equals L.
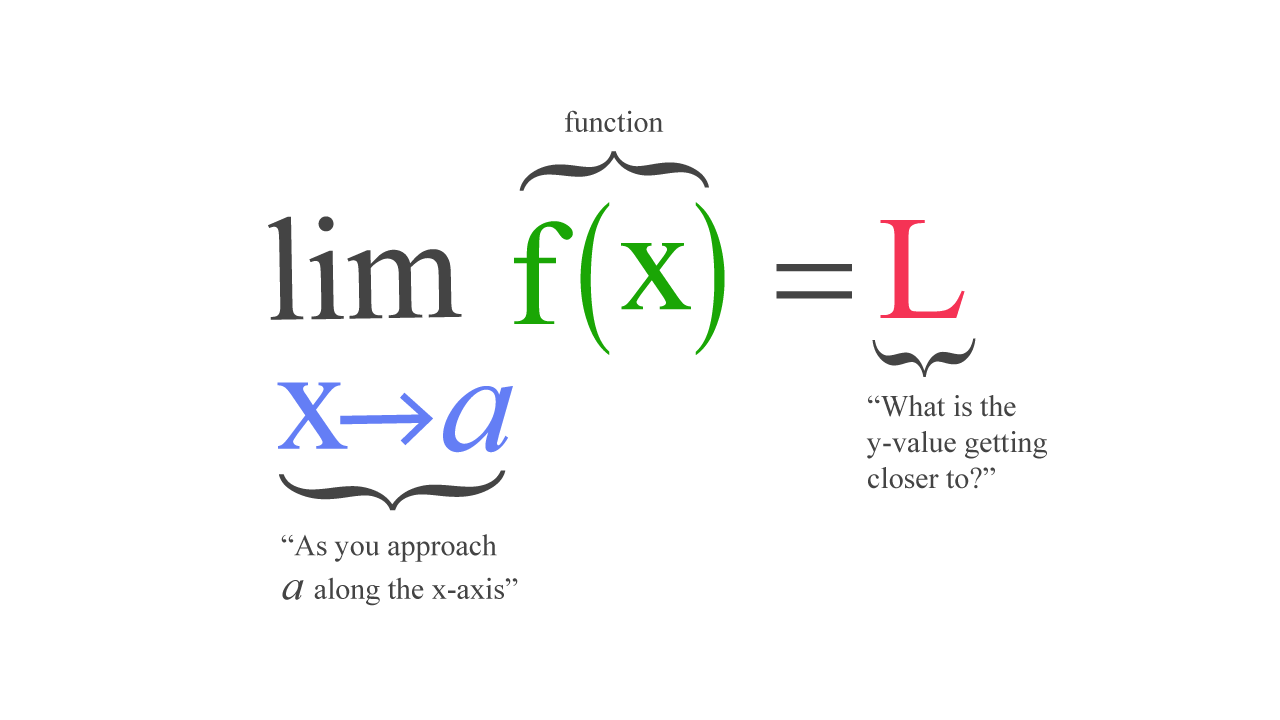
How to find a limit? – With steps
Limits can be applied as numbers, constant values (π, G, k), infinity, etc. Let’s go through a few examples to learn how to calculate limits.
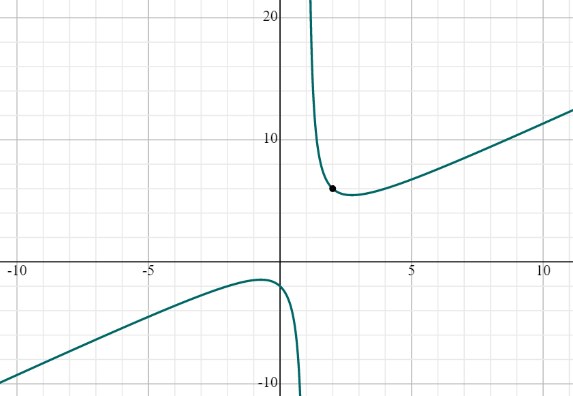
\(\lim _{x\to \:2^+}\frac{\left(x^2+2\right)}{\left(x-1\right)}\)
Solution:
A right-hand limit means the limit of a function as it approaches from the right-hand side.
Step 1: Apply the limit x➜2 to the above function. Put the limit value in place of x.
\(\lim \:_{x\to 2^+}\frac{\left(x^2+2\right)}{\left(x-1\right)}\)
\(=\frac{\left(2^2+2\right)}{\left(2-1\right)}\)
Step 2: Solve the equation to reach a result.
\(=\frac{\left(4+2\right)}{\left(2-1\right)} =\frac{6}{1} =6 \)
Step 3: Write the expression with its answer.
\(\lim \:_{x\to \:\:2^+}\frac{\left(x^2+2\right)}{\left(x-1\right)}=6\)
Graph
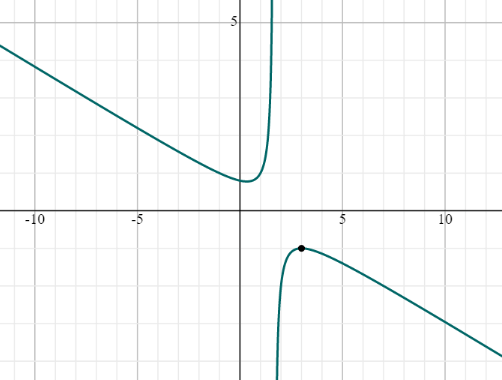
\(\lim _{x\to 3^-}\left(\frac{x^2-3x+4}{5-3x}\right)\)
Solution:
A left-hand limit means the limit of a function as it approaches from the left-hand side.
Step 1: Place the limit value in the function.
\(\lim _{x\to 3^-}\left(\frac{x^2-3x+4}{5-3x}\right)\)
\(=\frac{\left(3^2-3\left(3\right)+4\right)}{\left(5-3\left(3\right)\right)}\)
Step 2: Solve the equation further.
\(=\frac{\left(9-9+4\right)}{\left(5-9\right)}\)
\(=\frac{\left(0+4\right)}{\left(-4\right)} =\frac{4}{-4} =-1 \)
Step 3: Write down the function as written below.
\(\lim \:_{x\to \:3^-}\left(\frac{x^2-3x+4}{5-3x}\right)=-1\)
Graph
\( \lim _{x\to 5}\left(cos^3\left(x\right)\cdot sin\left(x\right)\right) \)
Solution:
A two-sided limit exists if the limit coming from both directions (positive and negative) is the same. It is the same as a limit.
Step 1: Substitute the value of the limit in the function.
\(\lim _{x\to 5}\left(cos^3\left(x\right)\cdot sin\left(x\right)\right)\)
\(=cos^3\left(5\right)\cdot \:sin\left(5\right)\)
Step 2: Simplify the equation as we did in previous examples.
\( \lim _{x\to 5}\left(cos^3\left(x\right)\cdot sin\left(x\right)\right) \)
\( =cos^3\left(5\right)\:sin\left(5\right)\)
Step 3: The above equation can be considered as the final answer. However, if you want to solve it further, solve the trigonometric values in the equation.
\(=\frac{1141}{50000}\cdot \:-\frac{23973}{25000} =-\frac{10941}{500000} \)
\(\lim \:\:_{x\to \:\:5}\left(cos^3\left(x\right)\cdot \:\:sin\left(x\right)\right)\)
\(=-0.021882 \)
Graph
FAQ’s
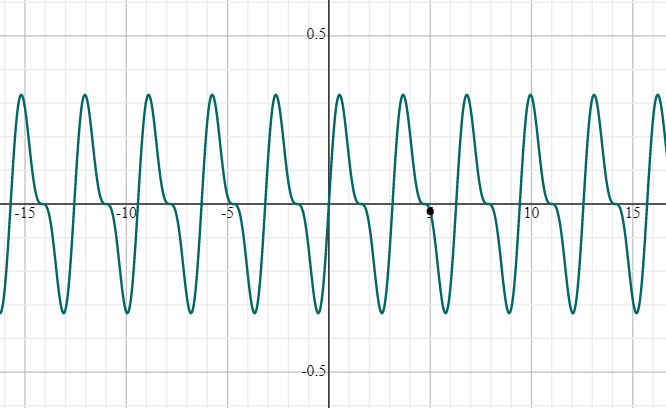
Does sin x have a limit?
Sin x has no limit. It is because, as x approaches infinity, the y-value oscillates between 1 and −1.
What is the limit of e to infinity?
The limit of e to the infinity (∞) is e.
What is the limit as e^x approaches 0?
The limit as e^x approaches 0 is 1.
What is the limit as x approaches the infinity of ln(x)?
The limit as x approaches the infinity of ln(x) is +∞. The limit of this natural log can be proved by reductio ad absurdum.
- If x >1ln(x) > 0, the limit must be positive.
- As ln(x2) − ln(x1) = ln(x2/x1). If x2>x1, the difference is positive, so ln(x) is always increasing.
- If lim x→∞ ln(x) = M ∈ R, we have ln(x) < M ⇒ x < eM, but x→∞ so M cannot be in R, and the limit must be +∞.
References
- What is limit calculus? Study.com | Take Online Courses. Earn College Credit. Research Schools, Degrees & Careers.
- Limits: A graphical approach - concept - calculus video by Brightstorm.
